Mathematik zwischen Schule und Hochschule
Die Dozenten des Mathematischen Instituts bieten regelmäßig interessante Vorträge für mathematisch interessierte Schülerinnen und Schüler an. Auf dieser Seite finden Sie einen Überblick der angebotenen Vorträge. Bei Interesse kontaktieren Sie bitte Frau Petra Kuhl (0641 99-32171, E-Mail: Petra.Kuhl@math.uni-giessen.de), um einen Termin zu vereinbaren.
In diesem Vortrag geht es um...
Karten mischen
Bei vielen Kartenspielen wie zum Beispiel Poker rechnen professionelle Spielerinnen bzw. Spieler ihre Chancen aus. Dabei gehen sie davon aus, dass jede Anordnung des Kartendecks gleichwahrscheinlich ist. Warum? Dürfen sie das? Bewirkt das Mischen der Karten tatsächlich, dass alle Anordnungen gleichwahrscheinlich sind und wenn ja, wie lange sollte dann gemischt werden?
Vortragender:
Matthias Meiners

Zielgruppe: Mittel- oder Oberstufe
Vorkenntnisse: Bruchrechnen
Zeitrahmen: idealerweise zwei Schulstunden (flexibel 45-90 Minuten)
Erforderliche Ausstattung: Beamer oder Videokonferenz
Format (max. Teilnehmerzahl): Vortrag mit Interaktion (max. 50 Personen)
Dieser Vortrag heißt...
Mit welcher Wahrscheinlichkeit stirbt eine Population aus
Heute ist es eine naheliegende und wichtige Frage, mit welcher Wahrscheinlichkeit das Eintragen einer ansteckenden Viruserkrankung in eine Gemeinschaft zu einem unkontrollierten Ausbruch führt. Die Mathematik stellt für solche Fragestellungen Modelle bereit. Das älteste geht auf Sir Francis Galton zurück, der sich im Jahr 1873 mit der Frage beschäftigte, mit welcher Wahrscheinlichkeit ein Familienname ausstirbt. Diese Frage unterscheidet sich aus mathematischer Sicht kaum von der Eingangsfrage und wurde von Reverend Henry William Watson, einem Zeitgenossen und Freund Galtons, untersucht und gelöst. Im Vortrag werden das Galton-Watson-Modell im historischen Kontext und im Kontext der Corona-Pandemie vorgestellt und die Aussterbewahrscheinlichkeit im Modell bestimmt.
Vortragender:
Matthias Meiners

Zielgruppe: Oberstufe
Vorkenntnisse: Funktionen, insbesondere Polynome; Ableitung; Verkettung von Funktionen; idealerweise: Grundkenntnisse in Stochastik
Zeitrahmen: idealerweise zwei Schulstunden (flexibel 45-90 Minuten)
Erforderliche Ausstattung: Beamer oder Videokonferenz
Format (max. Teilnehmerzahl): Vortrag mit Interaktion (max. 50 Personen)
Dieser Vortrag behandelt...
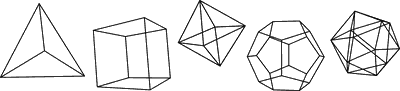
Die eulersche Polyederformel
Ein Würfel hat 8 Ecken, 12 Kanten und 6 Seiten und 8 - 12 + 6 = 2. Ein Tetraeder hat 4 Ecken, 6 Kanten und 4 Seiten und 4 - 6 + 4 = 2. Ausgehend von dieser Beobachtung entdecken wir, dass alle konvexen Polyeder die Formel von Euler erfüllen. Woher kommt das? Der Grund liegt letztlich nicht in der Kombinatorik von Polyedern, sondern in der Topologie der Sphäre...
Vortragender:
Stefan Witzel

Zielgruppe: Mittel- oder Oberstufe
Vorkenntnisse: keine; optional lineare Algebra und/oder vollständige Induktion
Zeitrahmen: 45-90 Minuten
Erforderliche Ausstattung: Beamer oder Viedokonferenz
Format (max. Teilnehmerzahl): Vortrag mit Interaktion (max. 40)
Dieser Vortrag heißt...
Sie haben Ihr Ziel erreicht
Wir haben uns daran gewöhnt, dass uns unser Navi oder Handy auf dem kürzesten Weg zu jedem beliebigen Ziel führen kann. Dieser Technik zugrunde liegt (neben GPS und gutem Kartenmaterial) ein erstaunlich einfacher Algorithmus des niederländischen Informatikers Edsger Dijkstra aus den 19 50er-Jahren. In diesem Vortrag werden wir Dijkstras Algorithmus neu entdecken.
W ir werden uns auch Probleme ansehen, die dem Problem, den kürzesten Weg zu finden, sehr ähnlich erscheinen, aber praktisch nicht gelöst werden können.
Vortragender:
Stefan Witzel

Zielgruppe: Mittel- oder Oberstufe
Vorkenntnisse: keine; optional etwas Graphentheorie
Zeitrahmen: idealerweise zwei Schulstunden (flexibel 45-90 Minuten)
Erforderliche Ausstattung: Beamer oder Videokonferenz
Format (max. Teilnehmerzahl): Vortrag mit Interaktion (max. 50 Personen)
Dieser Vortrag heißt...
Geheihmschriften und das Internet
Seit Jahrtausenden entwickeln Verschwörer, Verliebte, Spione und andere Techniken, um sich Nachrichten zu schicken, die andere nicht lesen können. Bis in die 1970er Jahre galt dabei eine Voraussetzung als unumgänglich: um sich geheime Nachrichten schreiben zu können, muss man vorher ein gemeinsames Geheimnis (einen „Schlüssel“ ) verabredet haben . Dieses Paradigma wurde 1976 durch das Diffie–Hellman-Protkoll widerlegt: es ermöglicht, mit fremden Personen, die man nie vorher gesehen hat, sicher verschlüsselte Nachrichten auszutauschen. Die asymmetrische Verschlüsselung war geboren. Erst später wurde bekannt, dass der britische Geheimdienst diese Technik bereits 1969 kannte.
Das heutige Internet wäre ohne asymmetrische Verschlüsselung undenkbar. Praktisch alle Kommunikation im Internet wird heute durch asymmetrische Verschlüsselung gesichert.
Im Vortrag werden wir das RSA-Verfahren kennenlernen, eines der verbreitetsten Verfahren zur asymmetrischen Verschlüsselung. Wir werden uns auch ansehen , wie Quantenmechanik die Sicherheit asymmetrischer Verfahren bedroht, aber auch neue Verschlüsselungstechniken ermöglichen kann.
Vortragender:
Stefan Witzel

Zielgruppe: Oberstufe
Vorkenntnisse: Rechnen modulo n ist hilfreich
Zeitrahmen: idealerweise zwei Schulstunden (flexibel 45-90 Minuten)
Erforderliche Ausstattung: Beamer oder Videokonferenz
Format (max. Teilnehmerzahl): Vortrag mit Interaktion (max. 50 Personen)
In diesem Vortrag geht es um...
Brain Reading – Gedankenlesen mit Methoden der Neuroinformatik?
Unsere Gedanken- und Erlebenswelten sind privat und für andere unzugänglich. Können wir mit Methoden der Gehirnforschung auch „von außen“ erkennen, was andere Menschen denken oder fühlen? In diesem Vortrag erkunden wir, wie Aufnahmen von Gehirnaktivität uns verraten können, was im Gehirn anderer vorgeht. Dazu lernen wir Methoden der Informatik und des maschinellen Lernens kennen, die es uns erlauben, statistische Vorhersagen über die Gedanken und das Erleben von Menschen zu treffen. Ausgehend von der Genauigkeit solcher Vorhersagen diskutieren wir praktische Anwendungen von Brain Reading, beispielsweise im klinischen oder kriminologischen Kontext, und fragen nach ethischen Gesichtspunkten beim Einsatz solcher Methoden.
Der Vortrag soll speziell die Anwendung von im Studiengang Data Science vermittelten Methoden der Mathematik und Informatik veranschaulichen.

Vortragender: Daniel Kaiser
Zielgruppe: Oberstufe
Vorkenntnisse: keine
Zeitrahmen: idealerweise zwei Schulstunden (flexibel 45-90 Minuten)
Erforderliche Ausstattung: Beamer oder Videokonferenz
Format (max. Teilnehmerzahl): Vortrag mit Interaktion (max. 50 Personen)
